백준 16958번 텔레포트 (c++)

 

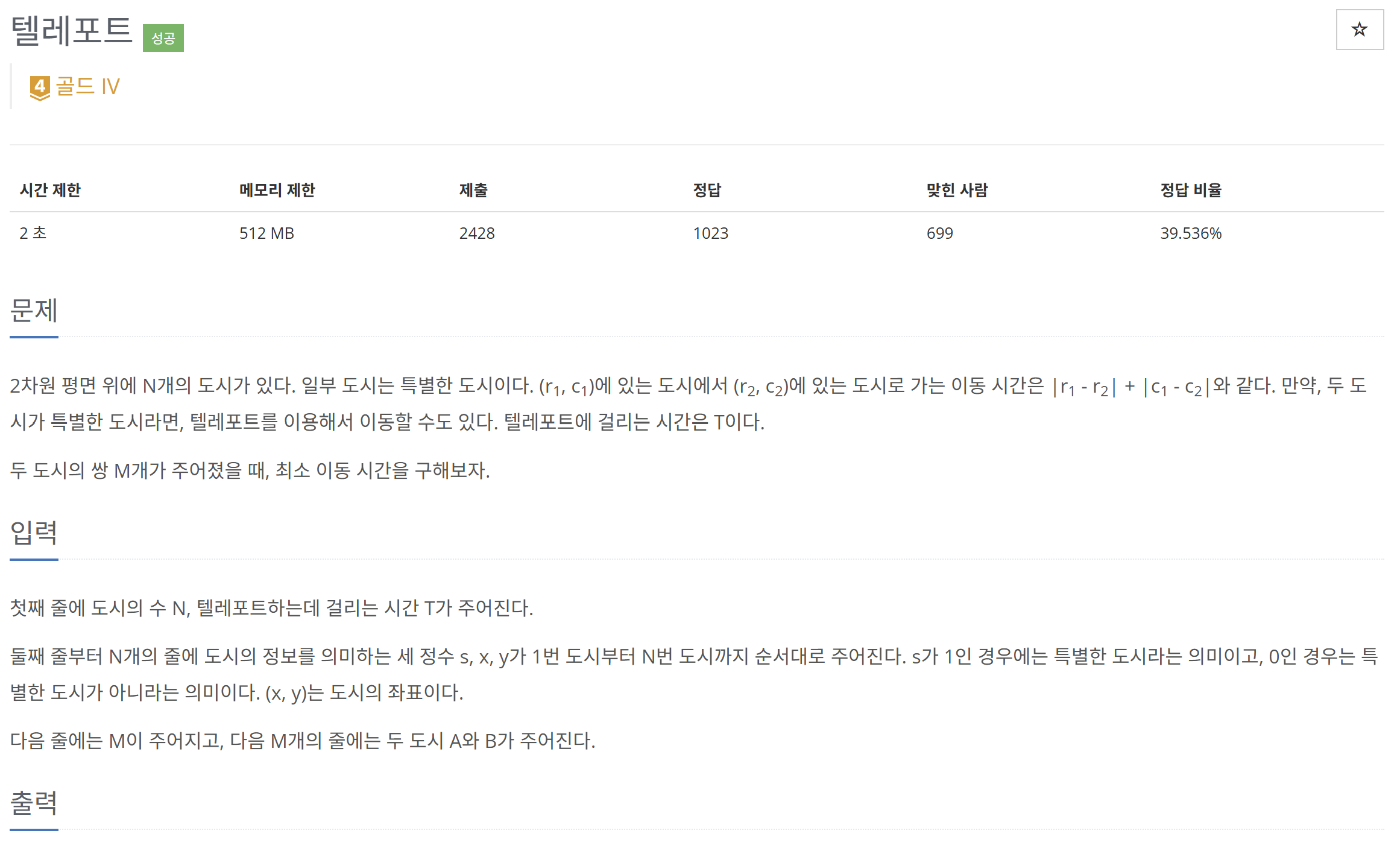
노드간의 최소 거리를 전부 구해놓고 출력만 하면 편할 것이고

텔레포트라는 개념도 있기 때문에 플로이드 워셜 알고리즘이 좋을 것이다.

 

void dist()
{
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			graph[i][j] = 2100000000;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		int r1 = city[i].first;
		int c1 = city[i].second;
		for (int j = 1; j <= n; j++)
		{
			if (i == j)
			{
				graph[i][j] = 0;
				continue;
			}
			int r2 = city[j].first;
			int c2 = city[j].second;
			graph[i][j] = abs(r1 - r2) + abs(c1 - c2);
			if (tele[i] == 1 && tele[j] == 1) graph[i][j] = min(graph[i][j], t);
		}
	}
}

노드간의 거리를 구해준다

텔레포트가 가능한 노드간의 경우 따로 처리를 해주는데, 주의할 점은

텔레포트 하는 시간 t보다 노드간 직접 이동하는 시간이 짧은 경우가 있기 때문에

잘 비교해주고 값을 넣는다

 

void calc()
{
	for (int k = 1; k <= n; k++)
	{
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (graph[i][k] + graph[k][j] < graph[i][j])
				{
					graph[i][j] = graph[i][k] + graph[k][j];
				}
			}
		}
	}
	
}

플로이드 워셜 알고리즘을 사용해준다.

 

int main()
{
	ios_base::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL);
	cin >> n >> t;

	for (int i = 1; i <= n; i++)
	{
		int s, x, y;
		cin >> s >> x >> y;
		city[i] = make_pair(x, y);
		tele[i] = s;
	}
	cin >> m;
	dist();
	calc();
	for (int i = 0; i < m; i++)
	{
		int a, b;
		cin >> a >> b;
		cout << graph[a][b] << endl;
	}
}

 

값을 출력해주면 된다

 

플로이드 워셜 알고리즘을 직접 사용하면 되는 간단한 문제